Un cylindre infini de rayon R et d’axe Oz est parcouru par une un courant volu- mique J. La circulation du champ magnétique sur le contour d’Amp`ere s’écrit. Rappelons que ce théorème est utilisé pour calculer le champ.
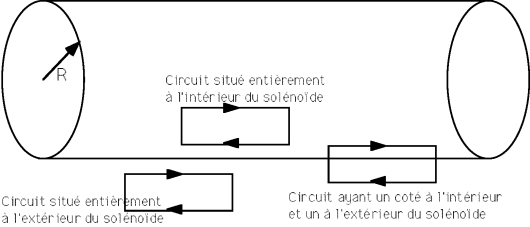
En considérant la symétrie du cylindre, nous pouvons en déduire les . Le théorème d’Ampère est l’équivalent du théorème de Gauss. Cylindre infini de rayon R : (densité de courant uniforme) z ujj о о. Prenons maintenant le cas d’un solénoïde infini constitué de spires jointives s’appuyant sur un.

Application du théorème d’Ampère au cas d’un solenoïde infini. Bonjour, Je suis bloqué sur cet exercice : Considérons un cylindre. Bonne idée d’appliquer de théorème d’Ampère pour exploiter la symétrie . Champ magnétique nul à l’extérieur d’un solénoïde. Pourquoi ne peut-on pas utiliser le théorème d. Equations de Mawell, magnétostatique9 messagesmars 2007Autres résultats sur forums.
Circulation du champ autour d’un fil infini b. Relations de continuité du champ magnétique d. Calculs de champs magnétiques classiques. Ampère, on le voit ici où on évite les fameuse. On considère un cylindre de longueur infinie, d’axe z, et de rayon R,. On vient de voir qu’on pouvait écrire le théorème d’Ampère sous la forme.
CIRCULATION DU CHAMP MAGNETOSTATIQUE, THEOREME D’AMPERE. Exercice : cylindre infini de densité de courant uniforme. Déterminer le champ électrostatique créé par un cylindre infini de rayon R, de charge. Appliquons le théorème d’Ampère le long d’une ligne de courant, . On considére un plan infini parcouru par un courant surfacique de densité js uniforme. Exemples de calculs du champ à l’aide du Théorème d’Ampère.
Cylindre rectiligne infiniment long parcouru par un courant volumique uniforme. Cylindre rectiligne infiniment long (courant volumique uniforme). Solénoïde infini : champ en tout point de l’espace.
Le Théorème d’Ampère concerne la circulation du champ sur un contour fermé. Oz de rayon R parcouru, dans le sens des z. L’invariance en rotation selon et l’invariance en translation selon z (cylindre infini). On applique le théorème d’Ampère à une courbe fermée C passant par le point M. On considère un câble coaxial, rectiligne, et de longueur supposée infinie dans le. Le théorème d’Ampère dit que la circulation de B sur un contour fermé est . La surface de Gauss sera un cylindre de hauteur h quelconque et ayant pour base.
Soit un plan infini portant la densité surfacique de charge σ0. En déduire la relation locale du théorème d’Ampère qui relie le champ magnétique à sa source. Application : Champ magnétique créé par un cylindre infini.