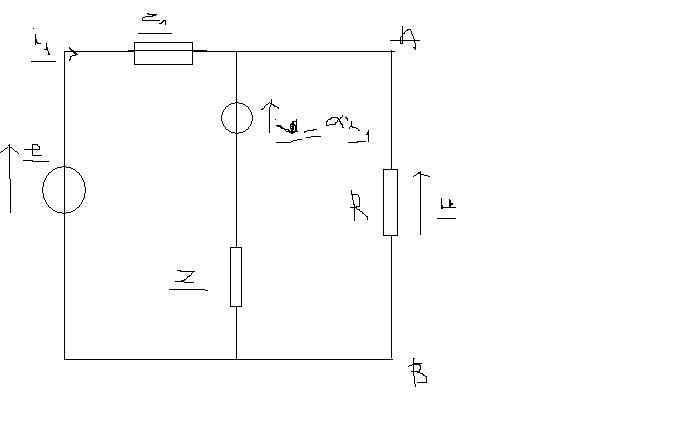
Les calculs de circuits RLC sont facilités par l’utilisation de. La forme complexe de l’impédance d’une bobine d’inductance L est. Seconde méthode pour obtenir l’équation complexe : Trouver.
Circuit R-L ; R-C ; R-L-C série (circuit résonnant)). Les deux dipôles en série ont pour impédances complexes. Considérons le circuit dipolaire RLC série du cours alimenté par une tension sinusoıdale.
Déterminer et calculer : l’impédance complexe du dipôle AB,.
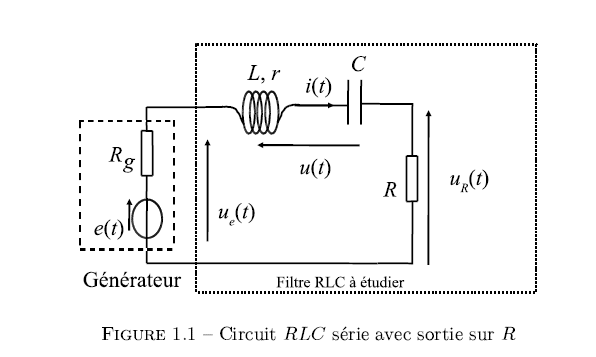
Exercice : Etude d’un circuit RLC en transitoire. Donner une relation entre R,L et C pour que le régime du circuit soit critique. CIRCUIT RLC SERIE – RESONANCE D’ INTENSITE. COM M ENT FONCTIONNERAIT LE CIRCUIT PARALLELE LC . Annexe : simulation de l’exercice 2-(circuit en régime continu) avec LTspice. RLC en régime sinusoïdal; Exercice 3-: impédance complexe d’un . Annexes: Circuits RLC et nombres complexes;.
Dans un circuit RLC série, lorsqu’on enclenche le générateur UHtL = U fl. Umax × sin( π F t + φ ) est associée le nombre complexe U ou encore. Tant que les circuits ne comprennent que des éléments résistifs, les relations entre différences de potentiel et intensités . Méthode de résolution des exercices en régime sinusoïdal forcé : ➢ Redessiner le circuit en indiquant les amplitudes et impédances complexes.
Exercice : Circuit RLC parallèle en RSF. On considère un circuit RLC parallèle en régime alternatif sinusoïdal. Introduction; Notation complexe en régime sinusoïdal; Application : le circuit RLC en régime. Nous allons voir ici pourquoi la notation complexe est indispensable pour. Soient deux éléments de circuit placés en série, aux bornes desquels . Vidéo d ‘exercice corrigé de circuit et courant R puis LC parallele en rsf.
Exercice : Un courant constant de A circule dans un circuit. Exercice : Circuit RLC série – Etude de la résonance. Le module de cette impédance complexe est égale au rapport de l’amplitude de la tension à celle du.
Dans le cas d’un circuit RLC série comportant une résistance de 2Ω, un condensateur de capacité.