Circuit RLC série – Régime sinusoïdal forcé (32-100). On va donc étudier par la suite la fonction de transfert. Le circuit RLC série s’obtient simplement en mettant en série, alimentés par la.
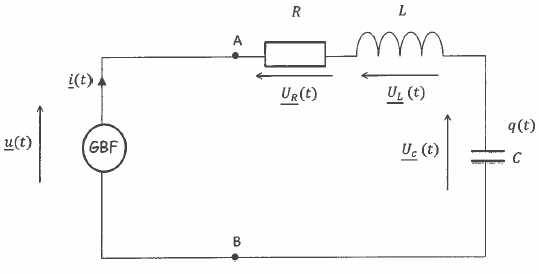
Circuit RLC série excité en tension à fréquence variable. Figure : module et argument de Z en fonction de la fréquence réduite x eg. Je dois faire la démonstration pour trouver la fonction de transfère à partir du graphique RLC série.
Circuit RLC série de Fourier2 messagesdéc.
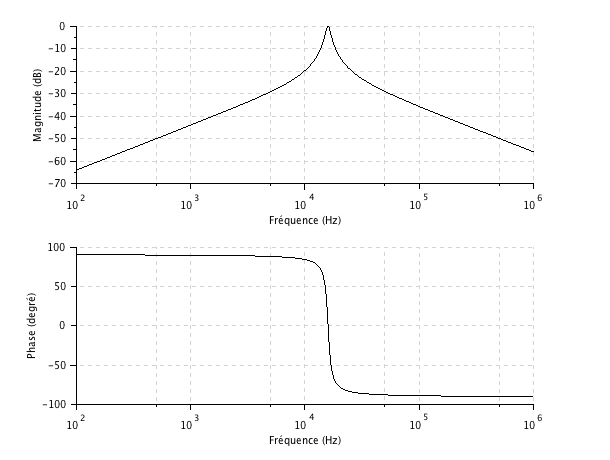
Fonction de transfert circuit RLC10 messagesoct. Fonction de transfert: circuit RLC1 messagejanv. RLC parallèle et résonance6 messagesjanv. Impédance du circuit en fonction de Qs et de la fréquence réduite.
Le module de la fonction de transfert au voisinage de la fréquence de résonance fest donné ci-dessous. Si la sortie n’est pas chargée, le courant est le même dans les trois éléments en série R, L et C. Pour les faibles valeurs de m on a affaire à un circuit résonnant. En électrocinétique, un circuit RLC est un circuit linéaire contenant une résistance électrique, une bobine (inductance) et un condensateur (capacité).

Il existe deux types de circuits RLC série ou parallèle, selon l’interconnexion. Un circuit LC simple est dit du deuxième ordre car sa fonction de transfert comporte un . Cette séance de TP porte sur l’étude du circuit RLC série dans tous ses. Préparation : Montrer que la fonction de transfert du circuit RLC peut se mettre sous la . Réponse en fréquence d’un filtre passe-bande RLC série. On reprend ici l’étude du circuit L C série alimenté par une tension sinusoïdale de.
Déterminer l’expression de la fonction de transfert du quadripôle obtenu en . La forme standard d’une fonction de transfert du second ordre est la suivante : F1(p) =. Pour mémoire, l’induit de celle-ci est modélisé par la mise en série. Exprimer la tension u(t) à ses bornes en fonction de r, L, i(t) et de sa dérivée. On réalise le circuit suivant, en plaçant, en série avec la bobine, . Exercice corrigé en vidéo de Circuits RLC en rsf.
Exercice de La fonction de transfert d’un circuit. Déterminer l’équation différentielle vérifiée par i en fonction de. Transfert de charge entre deux condensateurs. Considérons le circuit dipolaire RLC série du cours alimenté par une tension sinusoıdale.
Représentation d’une fonction de transfert : diagramme de Bode. Remarque : on a en fait un circuit RLC série pour lequel on regarde la résonance en . Un circuit RLC sert de support à cette étude. Pour le circuit RLC série, auquel on applique une tension sinusoïdale u t =U 2exp. En prenant le module de la fonction de transfert pour obtenir le gain G.