Reconnaître graphiquement les fonctions convexes et concaves. Utiliser le lien entre convexité et sens de variation de la dérivée. Une forme concave est une forme creuse : l’intérieur d’un bol par exemple.
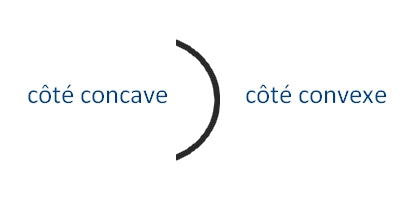
Une forme convexe est une forme bombée : un bol à l’envers par exemple. En géométrie, un polygone convexe est un polygone simple dont l’intérieur est un ensemble convexe. Un polygone simple qui n’est pas convexe est dit concave . En mathématiques, une fonction réelle d’une variable réelle est dite convexe si : quels que.

Une fonction concave est une fonction dont la fonction opposée est convexe. On vérifie aussitôt ce qui suit, reliant les notions d’ensemble convexe et . Le fait que l’on préfère commencer par définir la . L’étude d’une dérivée seconde permet de déterminer sur quels intervalles une fonction d’une variable est convexe ou concave et donc, entre autres . On dit qu’une fonction f est concave sur un intervalle I si et seulement si −f est convexe. Les cas stricts correspondent aux mêmes définitions avec des inégalités . Un polygone est convexe lorsqu’il n’y a pas d’angle rentrant ou de partie rentrante.
Une partie ou un angle rentrant est une partie qui rentre . Convexe : définition, synonymes, citations, traduction dans le dictionnaire de la langue française. Définition : Bombé, saillant vers l’extérieur. Un rappel de cours sur les fonctions convexes et les fonctions concaves. La fonction exponentielle x → ex est convexe sur R (voir figure 4).
Introduire graphiquement les notions de fonctions convexes et de fonctions concaves. La fonction sinus et la fonction cosinus ne sont ni convexes ni concaves. Comment définir une fonction convexe, une fonction concave ? Approche graphique Soit f une fonction dérivable sur un intervalle I. Avec a la concavité est orientée .