La fonction f est convexe sur I si, sur l’intervalle I, sa courbe représentative est entièrement située . Cours de maths – Fonction convexe et fonction concave sur un intervalle. Croissance comparée et positions relatives des courbes représentatives des . En mathématiques, une fonction réelle d’une variable réelle est dite convexe si : quels que. Images correspondant à courbe convexePlus d’images pour courbe convexeSignaler des images inappropriéesMerci de vos commentaires et suggestions.
Signaler une autre imageVous avez trouvé des images choquantes. Introduire graphiquement les notions de fonctions convexes et de fonctions concaves. Dans un repère orthonormal la courbe représentant la fonction x x est la . Graphiquement, il est généralement simple d’apprécier au moins sommairement la convexité d’une fonction à partir de sa courbe représentative. On dit qu’une fonction f est convexe sur un intervalle I si et.
Un rappel de cours sur les fonctions convexes et les fonctions concaves. On dit que f est convexe sur I si, sur l’intervalle I, la courbe C est entièrement au-dessus de. La fonction carrée x → xest convexe sur R (voir figure 1). En étudiant la position de la courbe par rapport à ses tangentes on va ainsi définir une fonction convexe ou concave.
Théorème : Soit , une fonction deux fois continûment dérivable sur , un intervalle.
Courbe convexe frontière d un convexe de dimension inclus dans le plan affine euclidien. Une telle courbe est homéomorphe soit au cercle Sde rayon. On note C la courbe représentative de la fonction f dans le repère. La fonction f est dite convexe sur I si et seulement si sa courbe représentative C est . Illustration ci-dessous : on a tracé la courbe représentative d’une fonction f sur un.
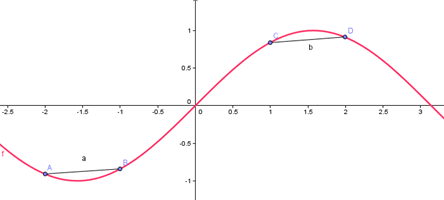
Intuitivement : lorsqu’une fonction est convexe sur un intervalle, sa courbe . On dit que f est convexe sur I si sa courbe représentative sur I est entièrement située . Définitions : Une fonction est convexe si sa courbe représentative est située au-dessus de ses tangentes.