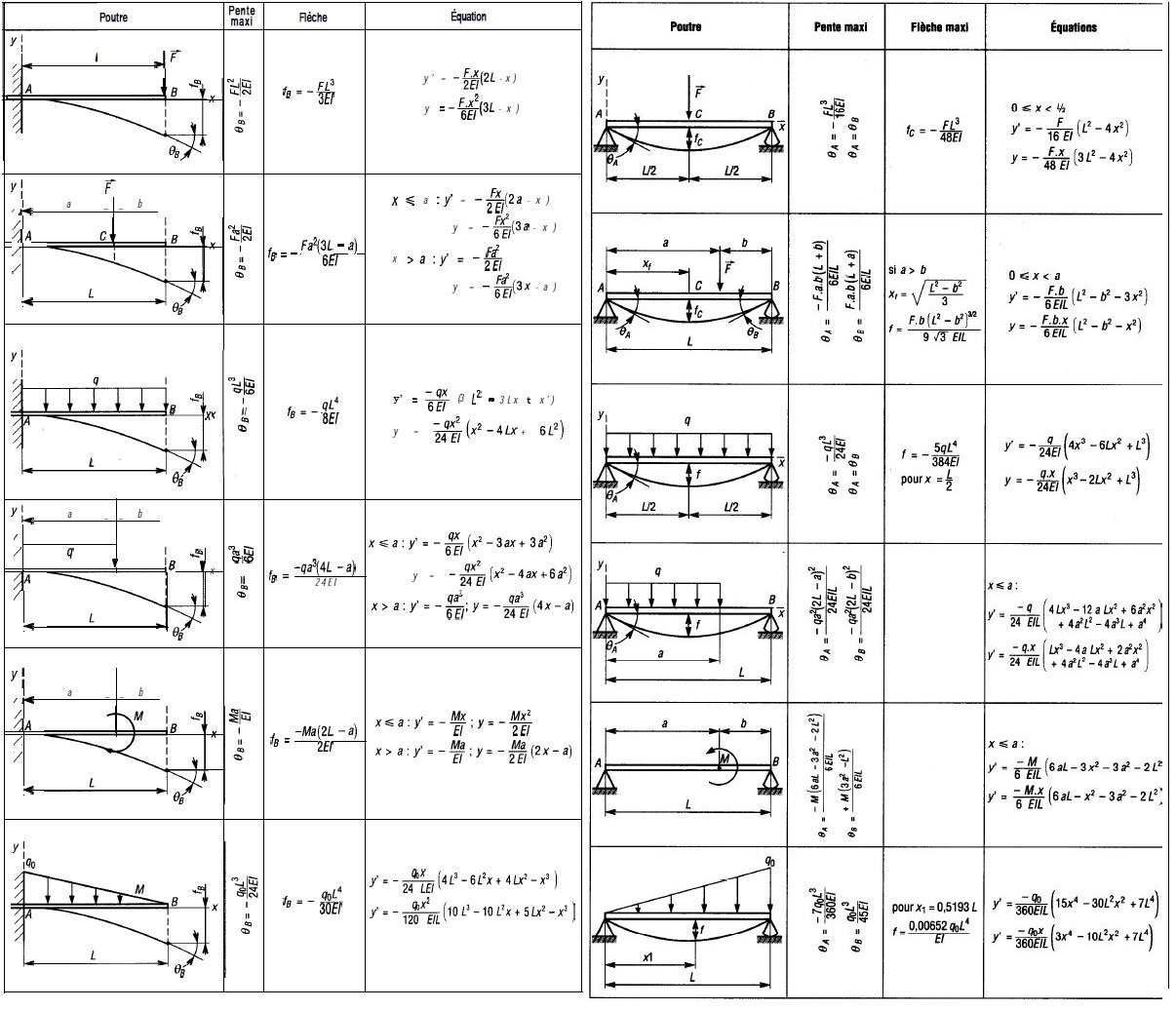
En résistance des matériaux, la flèche est usuellement la valeur maximale de la déformation acceptable (déformée) d’une poutre. En l’absence d’effort normal important, la déformée d’une poutre est liée au. Poutre sur deux appuis simples avec une charge uniformément répartie.

Poutre reposant sur deux appuis avec charge répartie. B) Poutre sur deux appuis soumise à une charge uniformément répartie sur la partie droite. Calcul de la flèche en un point : “Méthode différentielle”.
Intensité de la charge uniformément répartie par mètre de poutre.
Pour calculer la flèche et la contrainte de la poutre, rentrer les données. Poutre entre appuis, Poutre en porte à faux. On considère une poutre en sapin posée sur appuis distants de L = m. Expression du moment fléchissant Mz(x) pour un chargement uniformément réparti. On considère une charge de 2kg par m de poutre soit q = m g = 2× = 1960.
Identifier et surligner en rouge les éléments POUTRE sur. En utilisant le modèle mécanique précédent d’une poutre sur deux appuis soumise à une charge. La question a calculé la charge maximale répartie qui provoque la flèche . Le moment fléchissant induit une répartition de contrainte sur toute la section de la poutre, certaines fibres.

Hypothèses fondamentales de la théorie des poutres. Schéma des efforts appliqués à une poutre sur appui. Pour calculer la flèche f, on intègre deux fois l’équation.
Les réactions d’appuis R sont positives, les charges F négatives. Soit une poutre sur appuis soumise à forces Fet F les actions aux appuis sont A et. La charge peut aussi être répartie sur toute la longueur de la poutre . Il y a changement en entrant dans la poutre, après une charge concentrée ou réaction d’appui, en entrant dans une charge répartie, en rencontrant une . Une charge uniformément répartie sur une longueur est globalement . La poutre ABC est constituée d’un IPN de 5reposant sur appuis simples en B et C.