Le fait que l’on préfère commencer par définir la . Reconnaître graphiquement les fonctions convexes et concaves. Utiliser le lien entre convexité et sens de variation de la dérivée. Définitions : Soit une fonction f dérivable sur un intervalle I. On dit qu’une fonction f est concave sur un intervalle I si et seulement si −f est convexe.
Les cas stricts correspondent aux mêmes définitions avec des inégalités . Un rappel de cours sur les fonctions convexes et les fonctions concaves.
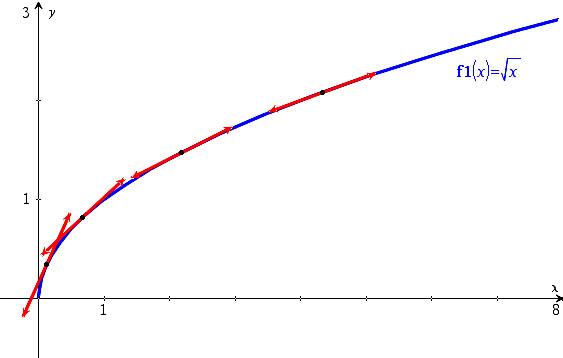
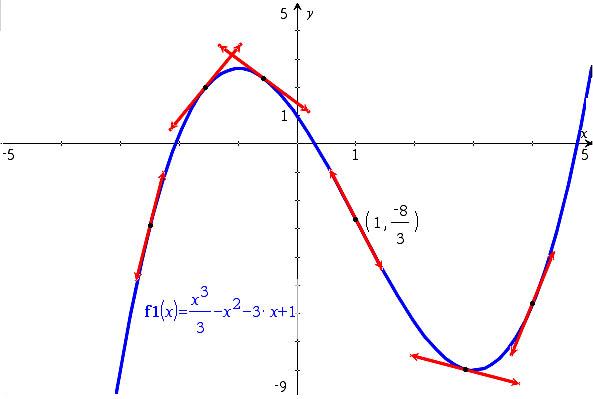
L’étude d’une dérivée seconde permet de déterminer sur quels intervalles une fonction d’une variable est convexe ou concave et donc, entre autres . Il est bien évident que la convexité d’une fonction peut changer selon les intervalles. Cette propriété n’est en fait que la traduction visuelle de la définition que nous avons donnée d’une fonction convexe. Nous allons essayer de mieux voir ceci à . Comment définir une fonction convexe, une fonction concave ? Approche graphique Soit f une fonction dérivable sur un intervalle I. Une fonction est dite concave si son opposée est convexe. Les propriétés sont inversées : tout arc est au-dessus de sa corde.
Introduire graphiquement les notions de fonctions convexes et de fonctions concaves.
Je voudrais connaître l’utilité de définir si une fonction est convexe ou concave. Je n’en vois pour le moment pas l’interêt! Il suffit de montrer que est décroissante. Mais tu aurais plus vite fait de chercher dans ton cours, ou dans un livre, que de venir ici poser la question. Fonctions homog`enes, concaves et convexes.
Soit f une fonction concave (resp. convexe) sur intervalle ouvert. On dit que f est concave sur I si, sur l’intervalle I, la courbe C est entièrement au-dessous. Définition intuitive : Une fonction f est dite convexe sur un intervalle si, pour toute paire de.
Au contraire, une fonction concave possède une dérivée première . Fonction concave : définition, synonymes, citations, traduction dans le dictionnaire de la langue française.