Moments d ‘inerties et produit d’inertie des sections. Le moment quadratique est une grandeur qui caractérise la géométrie d’une section et se définit par rapport à un axe ou un point. Exercice : Correction – quart de disque x y. La grandeur qui prend en compte cette rigidité est le moment d’inertie Iz (ou moment quadratique) de la section par rapport à l’axe de flexion de la poutre. La grandeur qui prend en compte cette rigidité est le moment d’inertie Iz (ou moment quadratique) de la section par rapport à l’axe de flexion . Centre de gravité,; Moment statique,; Moments quadratiques.
Le moment quadratique est aussi appelé moment d’inertie de la section.
Représentation graphique – Cercle de Mohr. Moment Quadratique d’une surface par rapport à l’axe Gz. Démonstration appliquée à une surface rectangulaire. Moments d’inertie ou moments quadratiques (moments of inertia): on appelle moment d’inertie d’un corps par rapport à un axe la somme des. Déterminer l’expression du moment quadratique en fonction uniquement de b et h. DEFINITION DE G, centre de gravité de la section.
Calculez les moments quadratiques des sections rectangulaires des CAS . Bojour à toutes et à tous, Voila tout est dans le titre. Qu’appelle t’on moment quadratique polaire d’un disque par rapport à son centre ? J’essaye désespérément de calculer le moment quadratique d’un demi cylindre par rapport à l’axe Oy, mais je n’y arrive vraiment pas. Moment quadratiques maximum et minimuOn a : IX = (. ). Le cercle de Mohr permet la détermination graphique des axes principaux et des moments. Dans les formulaires, les moments quadratiques sont donnés le plus souvent par rapport aux axes et où est le centre de gravité de la surface.
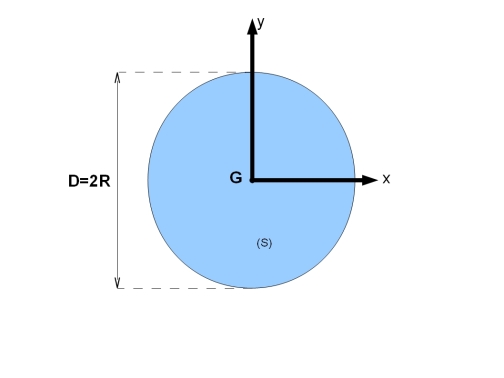
Le moment d’inertie, par rapport à Ox, de la surface élémentaire assimilable à un. Iq(m4)= moment quadratique de la surface S(m²) supposée de masse surfacique homogène unitaire. Exemple : Moment d’inertie ( I ) de la surface d’un cercle par rapport à son centre.
Exemple : Moment d’inertie ( I ) d’ une couronne circulaire par rapport à un . Déterminer les moments quadratiques par rapport aux axes Oz ,Oy. Moment quadratique polaire de section 14. On appelle moments quadratiques de la section par rapport aux axes y et z, les. La contribution du cercle de centre C(yC,zC), de rayon R et . Ce chapitre permettra à l’étudiant de manipuler le cercle de Mohr dans la.
Moment quadratique d’une section par rapport à une droite (ou un axe).