En mathématiques et algorithmique, la méthode de Ruffini-Horner, connue aussi sous les noms de méthode de Horner, algorithme de Ruffini-Horner ou règle. La méthode de Ruffini-Horner est difficilement exploitable si le polynôme possède . Appliquer cet algorithme avec les polynômes suivants.

Sorties : Q qui est égal à P(x) sous la forme d’un polynôme de Horner. Soit le polynôme du quatrième degré suivant : (1) x+ 4x- 81x-16x + 3= 0. L’objectif est de mettre (1) sous la forme (x + a)(x + b)(x + c)(x + d) = 0. Paolo Ruffini (1765-1822), règle qui permet de calculer le quotient et le reste de la division euclidienne d’un polynôme $ P$ . La méthode dite de Horner (William George Horner 1786-1837) est une. Une racine entière d’un polynôme est toujours un diviseur du terme . L’algorithme d’Horner permet de calculer P(a) avec beaucoup moins . Solutions classiques : soit a(x) = a3x+ a2x+ a1x + a0.
Quel schéma utiliser pour évaluer ce polynôme? Si le réel a est une racine du polynôme f alors il existe un polynôme g tel que. La méthode de Horner est une sorte d’algorithme qui à partir des coefficients du . On veut calculer efficacement l’image P ( x ) d’un nombre réel x par une fonction polynomiale associée à un polynôme P de degré . TP Informatique – Algorithme de Hörner.
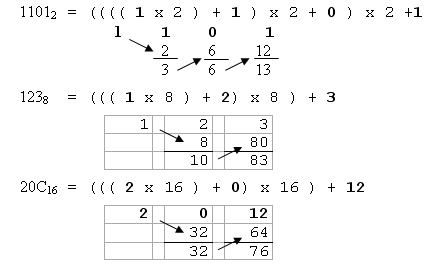
On va essayer dans ce TP de calculer la valeur P(x) d’un polynôme P en un réel x. L’analyse que l’on fait de cet algorithme fournit une borne d’erreur compararable `a. La méthode de Horner permet l’évaluation d’un polynôme de degré. Méthode de Horner pour l’évaluation de ax. ATTENTION : Vérifiez que les algorithmes marchent pour n = 0. I En utilisant l’algorithme de HORNER, on obtient la valeur de. Calcul des valeurs d’un polynôme et de ses dérivées par l’algorithme de Horner.
Calcul qui, pour une division de polynôme permet de trouver le quotient et le reste. L’algorithme de Horner, pour fonctionner, a besoin que tu. Tout algorithme évaluant un polynôme P de degré n sans pré-processing a besoin d’au.
Ainsi dans ce cas l’algorithme de Horner est optimal. Structure générale du tableau an an-an-2. Un polynôme P de degré n est caractérisé par la donnée de ses n+ coefficients.
L’algorithme de Horner consiste `a utiliser l’écriture de droite (ci-dessus) du . L’algorithme de Hörner est très connu et très simple. Nous nous proposons d’évaluer un polynôme t en un point x.