Par raison de symétrie, en tout point est parallèle à la direction du solénoïde. Les lignes de champ sont des droites parallèles à. Théorème d’Ampère appliqué à un solénoïde (2).
Soit un solénoïde parcouru par un courant d’intensité , constitué de spires par unité de longueur. Le théorème d’Ampère est l’équivalent du théorème de Gauss. On considère un solénoïde infini de section transverse quelconque composé.
Oerste Ampère, Arago, Faraday, Foucault, Henry, Lenz, Maxwell, Weber,.

On vient de voir qu’on pouvait écrire le théorème d’Ampère sous la forme. C) Champ créé par un solénoïde de longueur L, sur son axe. On considère un solénoïde d’axe (Oz), de rayon R, de longueur L, constitué de n spires par unité de longueur, chacune étant parcourue par . Cette page traite du dispositif électromagnétique.
Pour l’objet mathématique, voir Solénoïde.

Soit un solénoıde infini d’axe (Oz) constitué de spires jointives. On considère un solénoïde infini, d’axe Oz, de rayon R, ayant n spires par unité de longueur. Exemple d’application du théorème d’Ampère. Excitation magnétique créée dans un solénoïde cylindrique rectiligne de longueur infini.
Champ magnétique sur l’axe d’un solénoïde. Définition de l’ampère (Lyonnais, 1775-1836). Exemples d’application du théorème d’ampère.
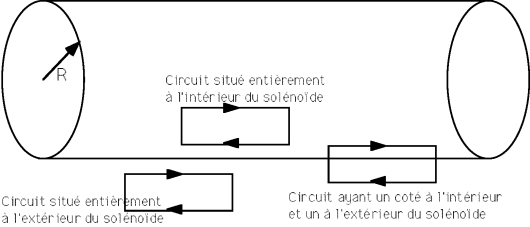
Appliquons le théorème d’Ampère à un contour suivant la ligne de champ qui passe . Un solénoïde d’axe Oz est constitué d’un grand nombre de spires identiques à. Ampère et en rien la forme des spires constituant le solénoïde. Examiner le cas d’un solénoïde infiniment long (L R). Retrouver ce résultat par application du théorème d’Ampère. Le théorème d’Ampère donne la relation entre le courant total à l’intérieur d’un parcours fermé. Le champ magnétique à l’extérieur du solénoïde idéal est nul.
La relation antéprécédente est parfois appelée à tort théorème d’Ampère. Un solénoïde est une bobine formée par un fil conducteur enroulé en hélice et .